| Cool Stuff: Fractals |
2008
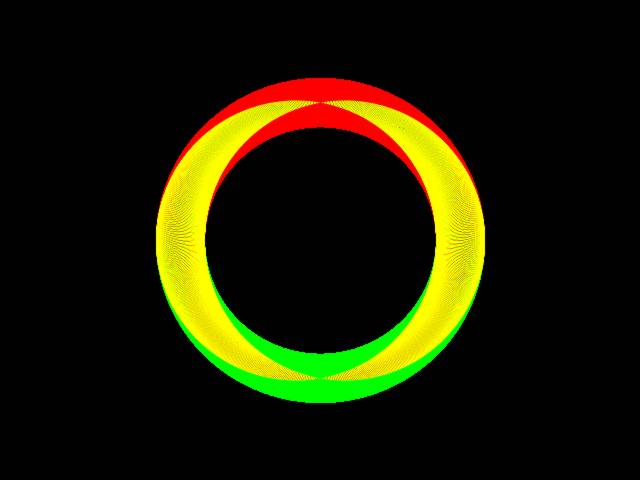
Cutting up doughnutsA cool thing about doughnuts that I didn't know until a few months ago was that you can always cut a doughnut so that its cross-section is two interlocking circles. 
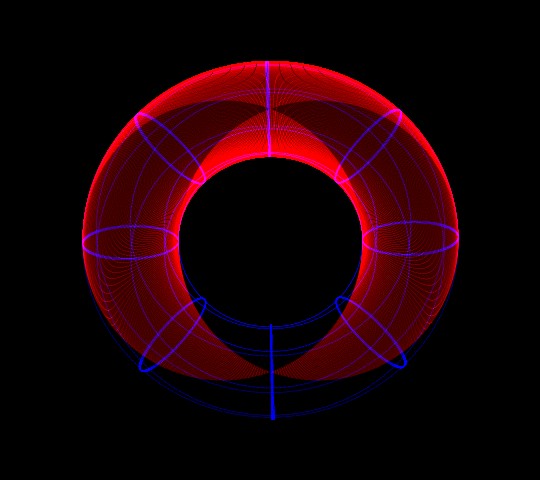
AnglesFirst, what's the magical cutting angle
that we have to use to get this cross-section, if we know the
proportions of the doughnut And that's enough for us to be able to work out the angle. After a few scribblings to work backwards from a couple of simple cases (angle 45 degrees, 60 degrees), it seems that if we know how fat the torus is (its minor radius, "r"), and we know how wide it is (measured from the centre to the centre of the ring limb, the major axis, "R"), the equation for the angle "A" for our cut turns out to be pretty simple. It's just : SIN A = r / R So as we transition between the two extremal shapes for the torus (from maximum skinny, r / R = 0, to maximum fatty, r / R = 1, r = R), the angle of the cut rotates nicely from zero degrees to 90 degrees. "Skinny torus" limitIf the thickness of the torus limb shrinks towards zero, we know that the two intersecting shapes MUST be perfect circles of radius R, because they don't have enough room to be anything else. At the limit of r / R = 0, when the surface shrinks to a one-dimensional line, curved around into a circle, we know that the overlap region for the two interlocking shapes has to be 100% ... because there's no room on the surface for the circles NOT to be totally overlapping.
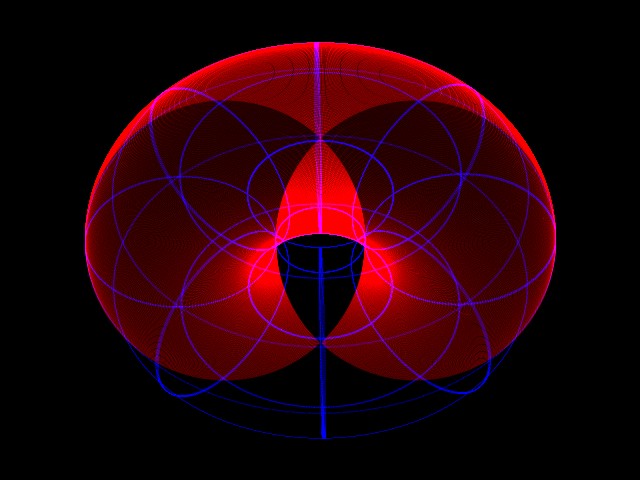
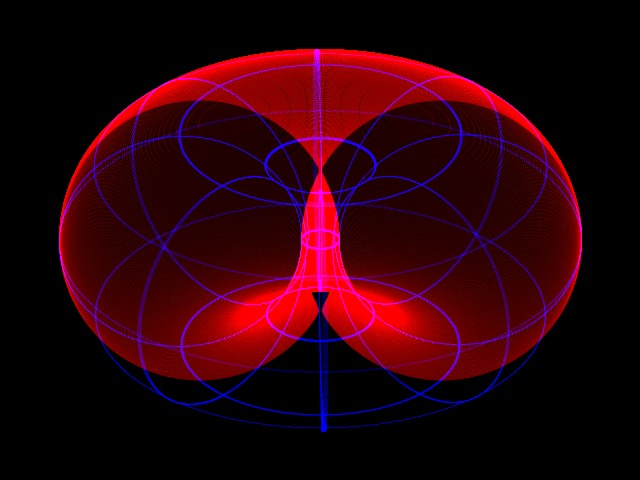
"Fat torus" limitAs "r" approaches the size of the major radius, R, the torus throat closes off. Our cross-section for this extremal case is simply a vertical slice through the torus centre, like so:
We have two
circles touching, of radius r
=
R ... so the two
circles are each exactly the same size as they were when they in the
skinny torus
limit. IntermediatesSo we can define the proportions of a torus by the special angle A (between 0 and 90 degrees) needed to cut it to get the double-circle. We also know that for 0<A<90, the two circles each slide around the shape so that they cross the outside equator of the torus on one side, and cross the opposing side of the inner equator on the other. These two points are always offset from the torus' inner circular minor axis, by the same distance (r), so we know that the width of the two individual intersecting shapes has to be constant. So if we keep R constant, and sweep the torus proportions over the full range, from r = 0 to r = R, and as the "special" cross-section angle tilts in sympathy from 0 to 90 degrees, the cross section is just a fixed-size pair of circles moving apart, from total overlap of 100%, to an overlap of zero.
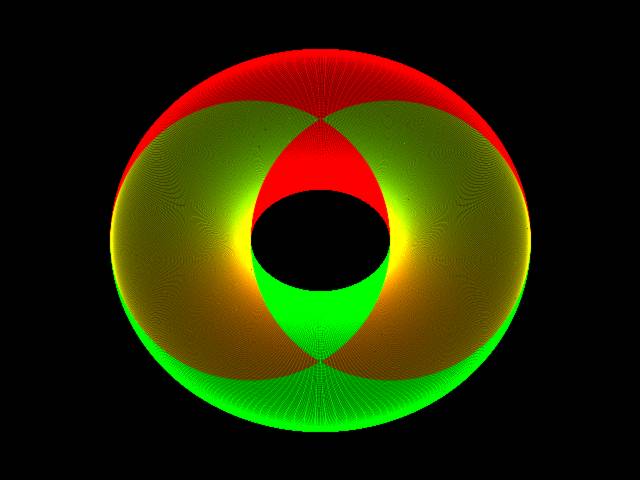
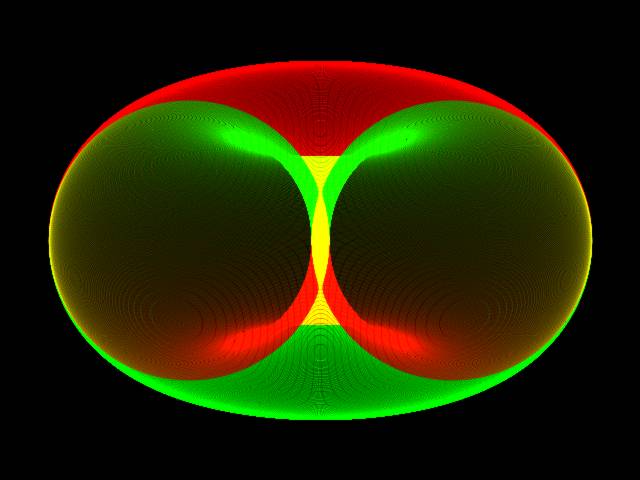
3D PlotsHere are a few plots of half-tori, all with different thicknesses and viewing angles, all sliced perpendicularly to the observer's view, to give the two-circle "linked rings" cross-section:Unlike the case of the chopped cube, I can't think of any wonderfully exciting practical applications for this yet, but, hey, maybe something'll hit me six months from now. Perhaps the result has special applications for building multiple intersecting toroidal particle accelerator arrays, or perhaps there's an application for using a Villarceau cage as an unconventional fusor frame. Or maybe not. I think I have too many other things that need doing to have the time to check this one out properly. External Links
copyright © Eric Baird 2009 |